Basic Info

Link

Cognitive Graph for Multi-Hop Reading Comprehension at Scale

Author

• Ming Ding
• Chang Zhou
• Qibin Chen
• Hongxia Yang
• Jie Tang

Basic Info

Link

Semi-supervised Learning on Graphs with Generative Adversarial Nets

Author

• Ming Ding
• Jie Tang
• Jie Zhang

Basic Info

Link

DeepInf: Social Influence Prediction with Deep Learning

Author

• Jiezhong Qiu
• Jian Tang
• Hao Ma
• Yuxiao Dong
• Kuansan Wang
• Jie Tang

Method(s)

Architecture

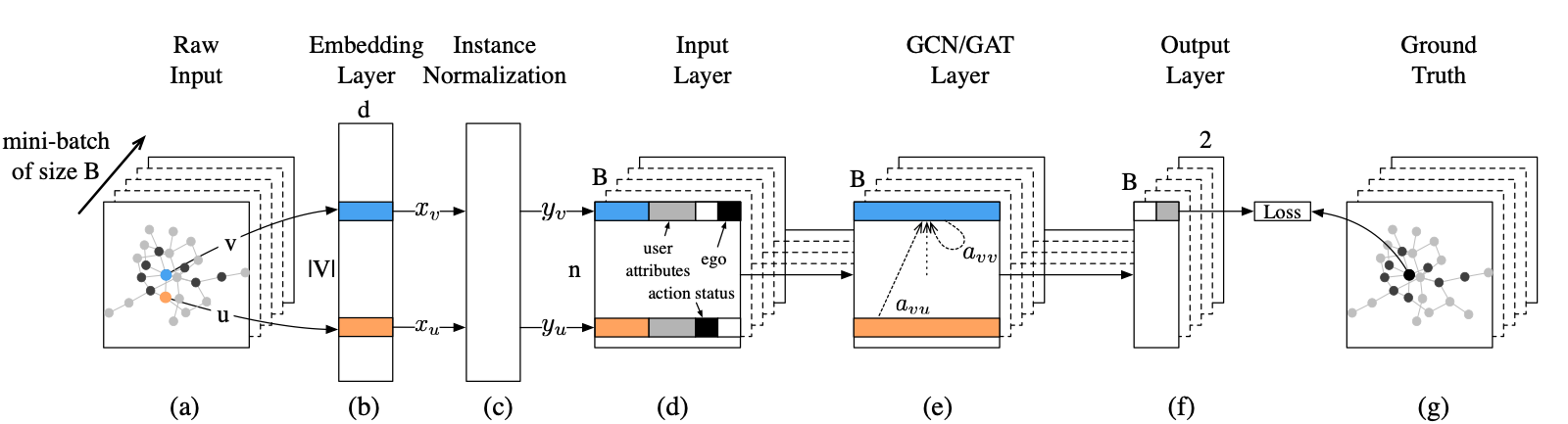
(a): Raw input which consists of a mini-batch of B instances; Each instance is a sub-network comprised n users who are sampled from the whole network. (b): An embedding layer which maps each user to a D-dimensional representation. (c): An Instance Normalization Layer which normalizes user’s embedding. (d): The formal input layer which concatenates together network embedding and other features. (e) A GCN and GAT Layer. (f) and (g) Compare model output and ground truth, we get the negative log likelihood loss. In this example, ego user v was finally activated (marked as black)

Reproduce

1. Background

Given input dimension \(d\), input data \(x\), \(y\) can be expressed as \(\vec{x} = (x_1, ... , x_d)\), \(\vec{y} = (y_1, ..., y_d)\), an SVM kernel function \(k(\vec{x}, \vec{y})\) can be expressed as the dot product of the transformation of \(\vec{x}\), \(\vec{y}\) by a transformation function \(\gamma\), that is to say

\[k(\vec{x}, \vec{y}) = \gamma(\vec{x}) \cdot \gamma(\vec{y})\]

2. Problems

Derive the transformation function \(\gamma\) for the following SVM kernels, also compute the VC Dimension for the SVM model based on these kernels.

• \(k(\vec{x}, \vec{y}) = (\vec{x} \cdot \vec{y})^n\)
• \(k(\vec{x}, \vec{y}) = (\vec{x} \cdot \vec{y} + 1)^n\)
• \(k(\vec{x}, \vec{y}) = e^{-\sigma(||\vec{x}||^2 + ||\vec{y}||^2)^n}\)

3. \(k(\vec{x}, \vec{y}) = (\vec{x} \cdot \vec{y})^n\)

根据多项式展开公式

\[k(\vec{x}, \vec{y}) = (\vec{x} \cdot \vec{y})^n = (x_1y_1 + x_2y_2 + \cdots + x_dy_d) ^ n = \sum{\frac{n!}{n_1!n_2!\cdots n_d!}{(x_1y_1)}^{n_1}{(x_2y_2)}^{n_2} \cdots {(x_dy_d)}^{n_d}}\]

所以

1. \(a_n = \sum\limits_{i=1}^{n}\frac{1}{i} = 1 + \frac{1}{2} + ... + \frac{1}{n}\)，数列\(\{a_n\}\)发散

\[\begin{align} a_n &= \sum\limits_{i=1}^{n}\frac{1}{i} \\ &= 1 + \frac{1}{2} + ... + \frac{1}{n} \\ &= 1 + \frac{1}{2} + (\frac{1}{3} + \frac{1}{4}) + (\frac{1}{5} + \frac{1}{6} + \frac{1}{7} + \frac{1}{8}) + ... \\ &> 1 + \frac{1}{2} + (\frac{1}{4} + \frac{1}{4}) + (\frac{1}{8} + \frac{1}{8} + \frac{1}{8} + \frac{1}{8}) + ... + \frac{1}{n} \\ &= 1 + \frac{1}{2} + \frac{1}{2} + ... \\ &= 1 + \frac{m}{2}​ \end{align}\]

其中\(m\)是\(\frac{1}{2}\)的个数，随着n的增大而增大

所以，

\[\lim\limits_{n\rightarrow\infty}a_n = \infty\]

2. \(|a_{n+p} - a_{n}| \le \frac{p}{n}, \forall n, p \in N^{*}\)，数列\(\{a_n\}\)发散

举反例，如数列\(\{1 + \frac{1}{2} + ... + \frac{1}{n}\}\)满足\(|a_{n+p} - a_{n}| \le \frac{p}{n}, \forall n, p \in N^{*}\)，但是其发散

3. \(|a_{n+p} - a_{n}| \le \frac{p}{n^2}, \forall n, p \in N^{*}\)，数列\(\{a_n\}\)收敛

\[\forall n, p \in N^{*}\]

\[\begin{align} |a_{n+p} - a_{n}| &\le |a_{n+p} - a_{n+p+1}| + |a_{n+p-1} - a_{n+p-2}| + ... + |a_{n+1} - a_{n}| \\ &\le \frac{1}{(n+p-1)^2} + ... + \frac{1}{n^2} \\ &\le \frac{1}{(n + p - 1)(n + p - 2)} + ... + \frac{1}{n(n - 1)} \\ &= \frac{1}{n-1} - \frac{1}{n+p-1} \\ &< \frac{1}{n-1} \end{align}\]

1. Problems

We take 0/1 classification problem for data with d dimensional features as an example. A neural network with one hidden layer can be written as

\[ o = w^T_2 σ(W_1v + b_1) + b_2 \tag{1}\]

where \(v\) is the \(d\) dimensional input feature of the data, while \(W_1\), \(w_2\), \(b_1\), \(b_2\) are the parameters of the neural network model. \(W_1\) is a \(n × d\) matrix, \(w_2\) is a n dimensional vector, and \(b_1\) is a \(n\) dimensional bias vector while \(b_2\) is the bias. When \(o > 0\) we classify the datum as label 1, while when \(o ≤ 0\) we classify it as label -1. This forms a neural network, or multi-layer-perceptron, with one hidden layer containing \(n\) neurons. In this problem, we focus on the pre-training case with frozen parameters that \(W_1\) and \(b_1\) must be decided when seeing all \(v\) without labels \((l_1, ...l_i)\), while \(w_2\) and \(b_2\) can be decided after seeing all labels of examples \((l_1, ...l_i)\)

1.1 Problem1

Given \(n, d\), calculate the VC dimension of the neural network for the linear activation case, i.e. \(\sigma(x) = x\). Prove your result.

1.2 Problem2

Given \(n, d\), calculate the VC dimension of the neural network for the \(ReLU\) activation case, i.e. \(\sigma(x) = max(0, x)\). Prove your result.

1.3 Hints

• Recall the definition of VC dimension.
• Consider \(n > d\) and \(n ≤ d\).
• For problem 2, Start from \(d = 1\)

Basic Info

Link: ImageNet Classification with Deep Convolutional Neural Networks - NIPS

Author:

• Alex Krizhevsky, University of Toronto
• Ilya Sutskever, University of Toronto
• Geoffrey E. Hinton, University of Toronto

Summary

Research Objective

作者的研究目标。

Problem Statement

问题陈述，要解决什么问题？

Method(s)

对C的扩展

#import

可保证头文件只被包含一次，无论此命令在那个文件中出现了多少次

NSLog 和@字符串

NSLog类似于C语言的printf()，添加了例如时间戳、日期戳和自动附加换行符等特性

NS前缀是来自Cocoa的函数，@符号表示引用的字符串应作为Cocoa的NSString元素来处理

NSArray提供数组，NSDateFormatter帮助用不同方式来格式化日期，NSThread提供多线程编程工具，NSSpeechSynthesizer使听到语音

使用NSLog()输出任意对象的值时，都会使用%@格式说明，使用这个说明符时，对象通过一个名为description的方法提供自己的NSLog()形式

Boolean类型

相比于C语言的bool类型，OC提供BOOL类型，具有YES(1)值和NO(0)值，编译器将BOOL认作8位二进制数

Basic Info

Link: arXiv:1311.2524

Author: Ross Girshick, Jeff Donahue, Trevor Darrell, Jitendra Malik

Summary

Research Objective

作者的研究目标。

Problem Statement

问题陈述，要解决什么问题？

Method(s)

解决问题的方法/算法是什么？

1. 基本形式

给定由\(d\)个属性描述的示例\(\boldsymbol{x}=(x_1;x_2;…;x_d)\)，其中\(x_i\)是\(\boldsymbol{x}\)在第\(i\)个属性上的取值，线性模型试图学得一个通过属性的线性组合来进行预测的函数，即

\[f(\boldsymbol{x})=w_1x_1+w_2x_2+…+w_dx_d+b \tag{3.1}\]

一般用向量形式写成

\[f(\boldsymbol{x})=\boldsymbol{w}^T\boldsymbol{x}+b \tag{3.2}\]

其中\(\boldsymbol{w}=(w_1;w_2;…;w_d)\)。\(\boldsymbol{w}\)和\(b\)学得之后，模型就得以确定

2. 线性回归

给定数据集\(D={(\boldsymbol{x}_1,y_1), (\boldsymbol{x}_2,y_2),…,(\boldsymbol{x}_m,y_m)}\)，其中\(\boldsymbol{x}_i=(x_{i1}, x_{i2},…,x_{id}), y_i\in\mathbb{R}\)，"线性回归"(linear regression)试图学得一个线性模型以尽可能准确地预测实值输出标记。

我们先考虑一种最简单的情形：输入属性的数目只有一个。为便于讨论，此时我们忽略关于属性的下标，即\(D=\{(x_i,y_i)\}_{i=1}^m\)，其中\(x_i\in\mathbb{R}\)，对于离散属性，若属性值之间存在"序"(order)的关系，可通过连续化将其转化为连续值；若属性值间不存在序关系，假定有\(k\)个属性值，则通常转化为\(k\)维向量。

线性回归试图学得